You are here
平成24-25年度 採択課題 実施概要
TSUBAMEグランドチャレンジ大規模計算制度の採択課題は、実施終了後1ヶ月以内に実施報告書を提出します。実施報告書のうち、速報の役割を果たす実施概要を下記に公開します。
最終成果報告書は実施終了後1年以内に提出され、「採択情報 / 成果報告書」のページにて公開されます。
平成24年度秋期 採択課題
格子ボルツマン法による1m格子を用いた都市部超高解像度気流シミュレーション
[利用課題責任者]
東京工業大学 学術国際情報センター
青木 尊之 教授
[利用カテゴリ]
カテゴリA (全ノード利用)
都市は高層ビルが立ち並び複雑な構造をしており、詳細な気流を解析するためには高解像度格子による大規模気流計算が必要となる。計算手法は GPUコンピューティングおよび大規模計算に適した格子ボルツマン法を用いた。都市の気流はレイノルズ数が100万を超えるような乱流状態になるため、ラージエディ・シミュレーション(LES)の乱流モデルを導入する必要がある。本研究では、モデル定数を局所的に決定できるコヒーレント構造スマゴリンスキー・モデルを格子ボルツマン法に導入し、大規模な気流のLES計算を始めて可能にした。CUDA を用いてコードを実装し、並列計算の大きなオーバーヘッドとなるGPUのデバイス・メモリ間の通信を分割領域内の計算とのオーバーラップにより実行性能を 30% 以上向上させた。1,000 GPUを用いた計算ではピーク性能の 15% となる 149 TFLOPSの実行性能が得られた。10,080 × 10,240 × 512 格子に対して 4,032 個の GPU を用い、新宿や皇居を含む 10km 四方のエリアを 1m 格子で計算した。外挿すると、約 600 TFLOPS の実行性能が得られたと推測できる。また、電力性能についても545 MFLOPS/Watt という高い数値を達成できた。これにより、高層ビル背後の発達した渦によるビル風や幹線道路に沿って流れる「風の道」、台風の際の被害などが飛躍的な精度で予測できるようになる。

Figure 東京都心気流計算結果
新カーネルを取り入れた大規模グラフ処理ベンチマーク Graph500 のスケーラブルな探索手法による性能評価
[利用課題責任者]
東京工業大学 情報理工学研究科
鈴村 豊太郎 客員准教授
[利用カテゴリ]
カテゴリA (全ノード利用)
Graph500ベンチマークとは,スーパーコンピュータのグラフ処理性能を測定する新しいベンチマークである.スパコンのベンチマークでは,数値計算性能を測るLinpackによるTop 500が有名だが,近年,大規模グラフ処理が,重要性を増しており,Graph500ベンチマークが広がりを見せている。Graph500ベンチマークは、大規模グラフに対する幅優先探索(BFS)の計算速度を計測し、1秒間に辿った枝の数(TEPS)を性能指標として、ランキングを出す。本GCでは、Graph500 BFSのGPU実装のパラメータを調整することにより、前回より性能を向上させることに成功し、問題サイズSCALE 35で431 GTEPSの性能を達成した。また、Graph500に新しく導入が予定されている単一始点最短経路問題(Single Source Shortest Path, SSSP)を計算するプログラムを作成し、性能評価を行った。結果、SSSPにおいても隣接行列の2次元分割が有効であることが分かり、また、SSSPにおいてはプロセス間の同期コストが全体の性能に大きく影響することが分かった。
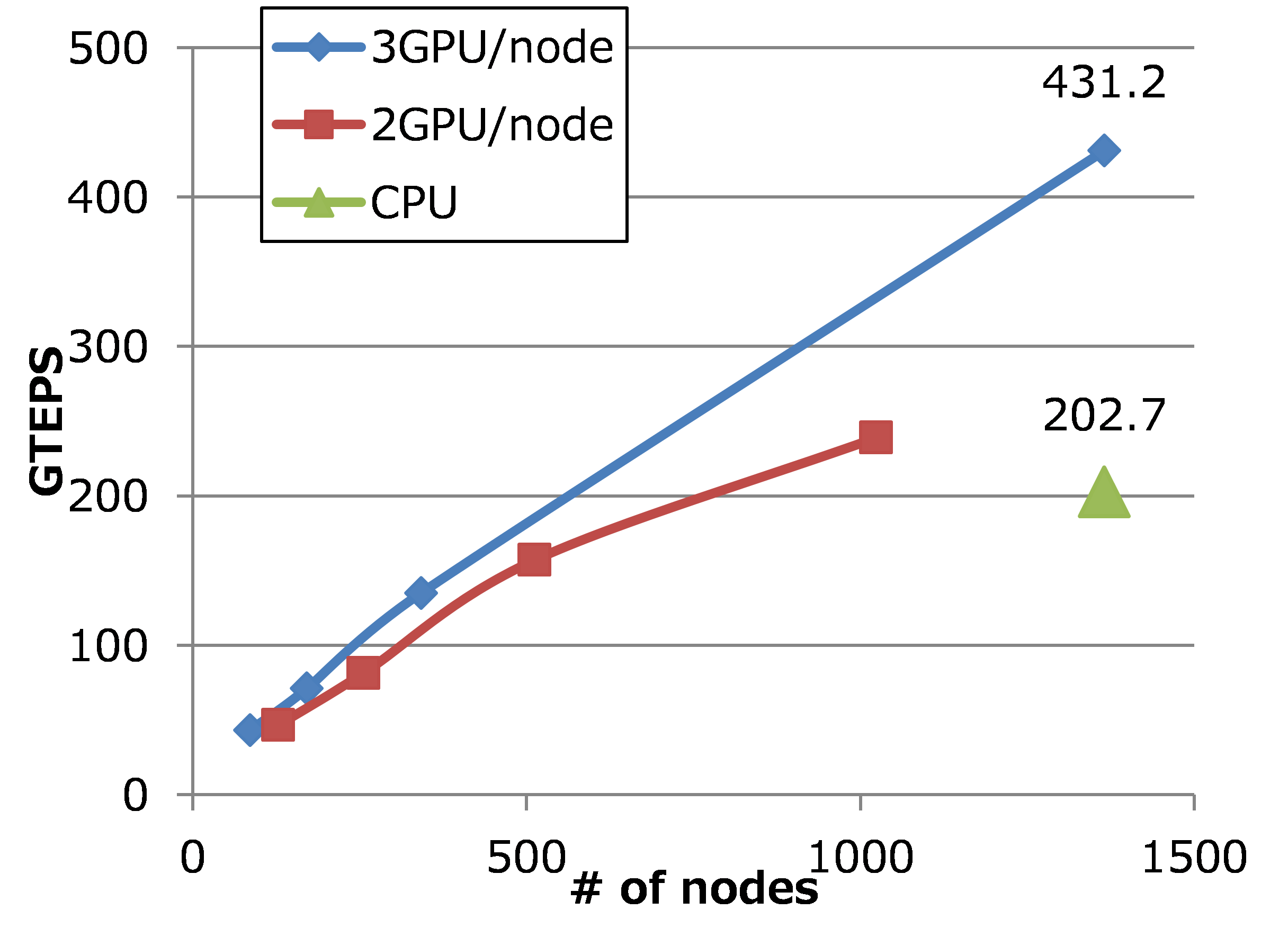
Figure TSUBAME2.0におけるGraph500ベンチマークの性能
平成24年度春期 採択課題
大規模グラフ処理ベンチマーク Graph500 のスケーラブルなGPU実装による性能評価
[利用課題責任者]
東京工業大学 情報理工学研究科
鈴村 豊太郎 客員准教授
[利用カテゴリ]
カテゴリA (全ノード利用)
Graph500ベンチマークとは,スーパーコンピュータのグラフ処理性能を測定する新しいベンチマークである.スパコンのベンチマークでは,数値計算性能を測るLinpackによるTop 500が有名だが,近年,大規模グラフ処理が,重要性を増しており,Graph500ベンチマークが広がりを見せている。Graph500ベンチマークは、大規模グラフに対する幅優先探索(BFS)の計算速度を計測し、1秒間に辿った枝の数(TEPS)を性能指標として、ランキングを出す。本GCでは、BFSの2次元分割による分散処理に対して、効率の良いアルゴリズムを考案し、CPUのみで計算する実装と、GPUを利用した実装の2つを作成し、性能評価を行った。CPU実装は、問題サイズScale 37(頂点数1374億個、枝数2.2兆個)のグラフの幅優先探索を10.85秒で計算し、計算速度203GTEPSを達成し、GPU実装は、問題サイズScale 35(頂点数344億個、枝数0.55兆個)グラフの幅優先探索を1.73秒で計算し、計算速度317GTEPSを達成した。
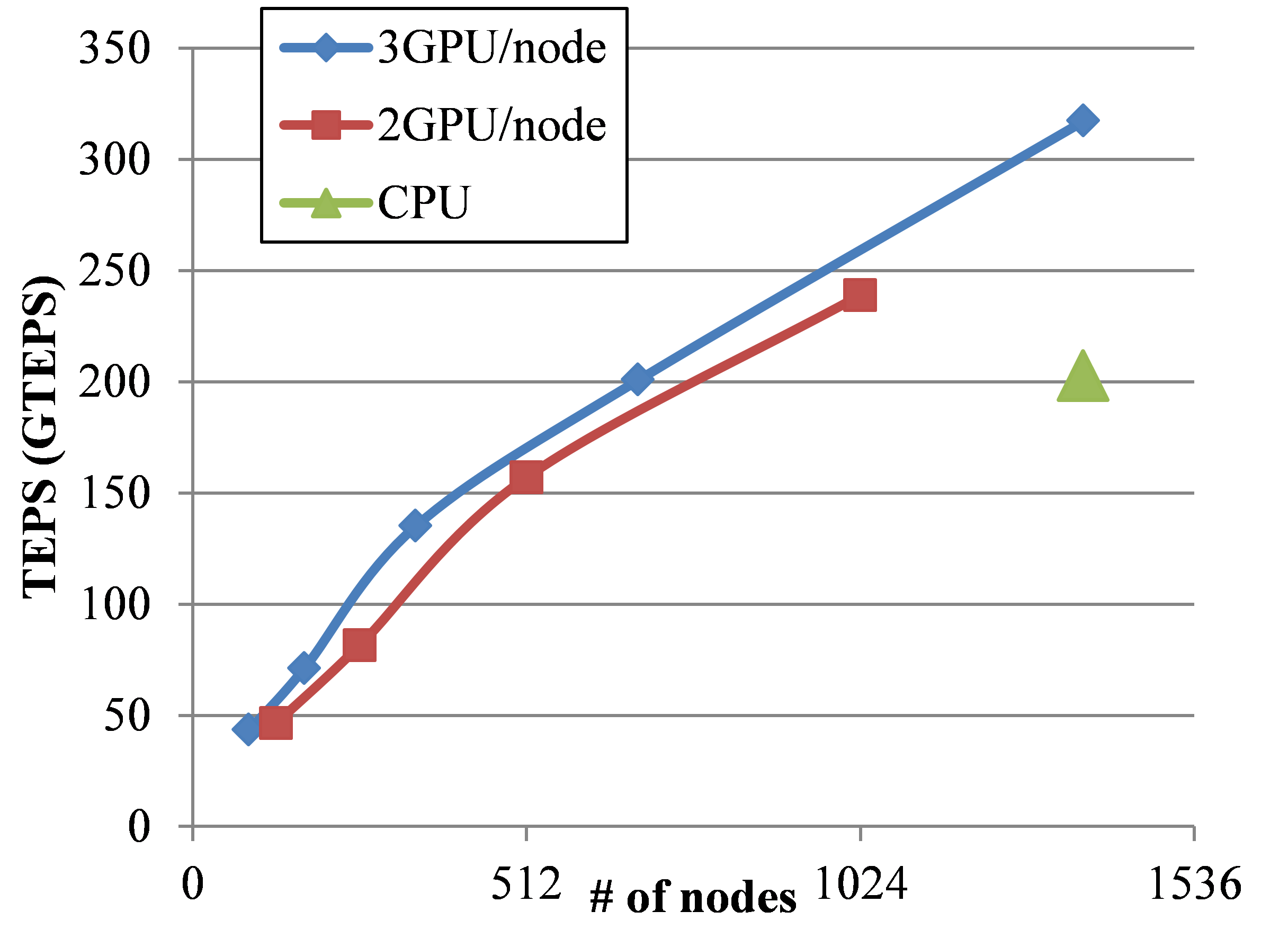
Figure TSUBAME2.0におけるGraph500ベンチマークの性能
内点法アルゴリズムの並列計算による超大規模半正定値計画問題の解決
[利用課題責任者]
中央大学理工学部
藤澤 克樹 教授
[利用カテゴリ]
カテゴリA (全ノード利用)
半正定値計画問題(SDP)は組合せ最適化, システムと制御, データ科学, 量子化学など非常に幅広い応用を持ち、様々な分野で最も注目されている最適化問題の一つとなっている。今後のエネルギー供給計画(スマートグリッド等)では非線形の複雑な最適化問題を扱う必要があり、SDPの高速計算技術の確立が急務である。
SDP に対しては高速かつ安定した反復解法である内点法アルゴリズムが存在しているが、巨大な線形方程式系の生成と計算が大きなボトルネックとなっている。申請者のグループでは、疎性の追求、計算量やデータ移動量などによる計算方法の自動選択などの技術を他に先駆けて実現し、すでに上記のボトルネックの高速化と世界最大規模の SDP を高速に解くことに成功している。今回の利用課題では主要なボトルネックの一つである線形方程式系のCholesky分解に対して、多数GPUの活用や計算と通信のオーバーラップ技術を応用することによって(図1)、制約式の数が148万以上となる 世界最大規模の巨大 SDP(図2) を解きSDPの世界記録の更新及び最大で533TFlops(Cholesky分解:4080 GPU)の性能を達成した(図3)。
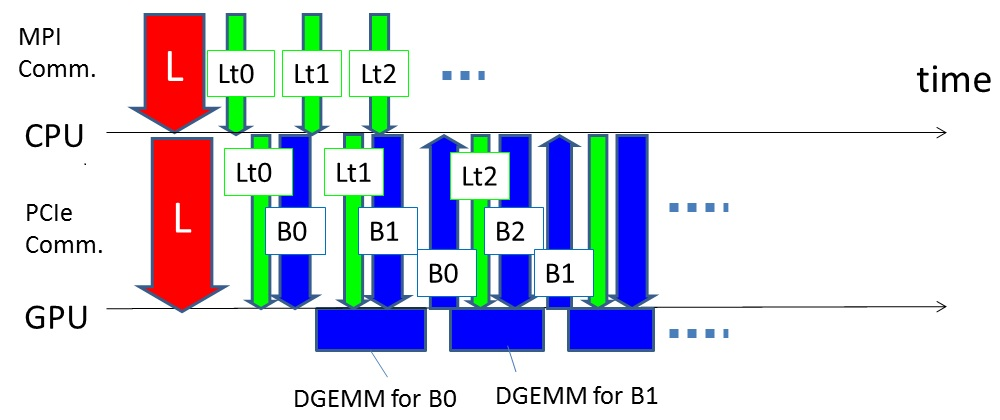
図1 GPU での計算、PCIe 経由の通信及び MPI 通信のオーバーラップ
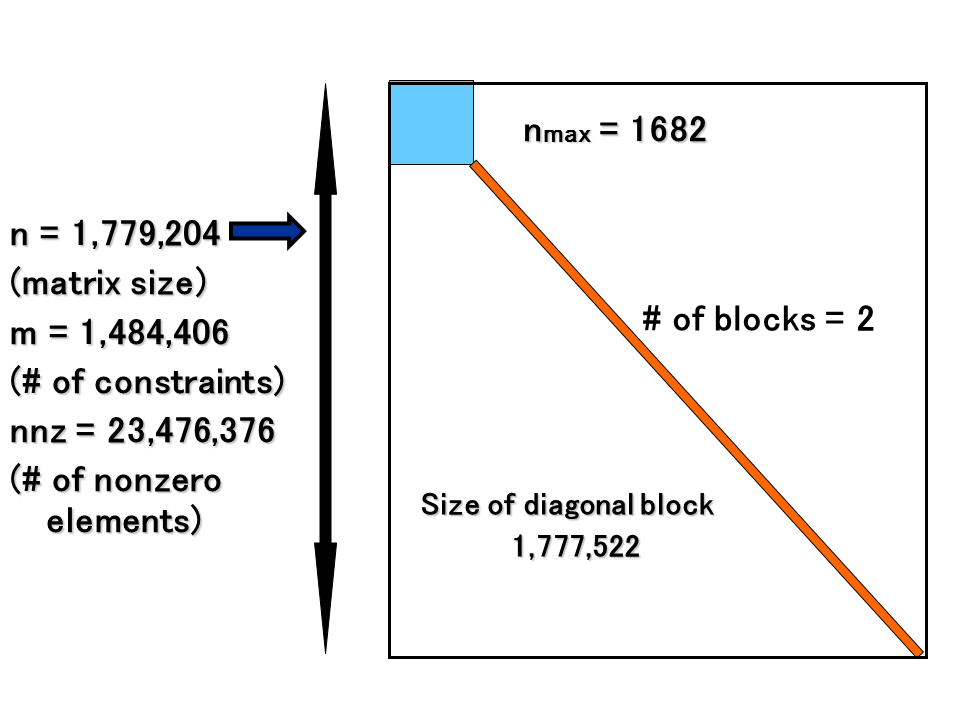
図2 世界最大規模のSDPとそのブロック対角構造
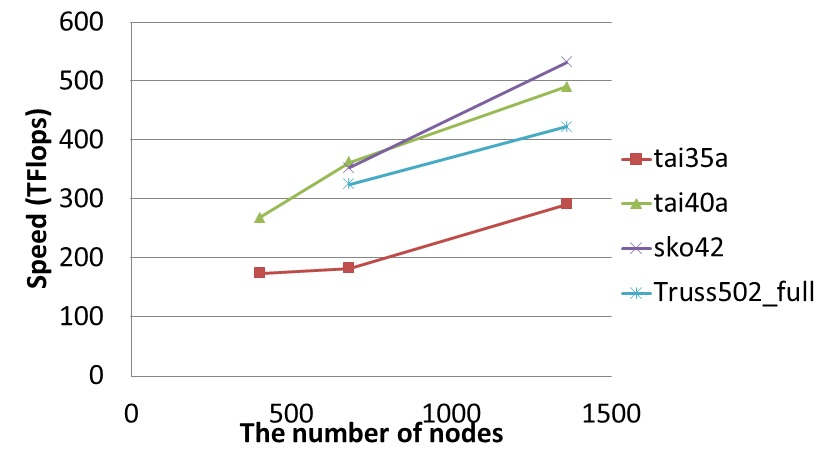
図3 TSUBAME2.0 上でのCholesky分解の性能(1,360ノード, 4,080 GPU)
平成25年度春期 採択課題
超並列計算機TSUBAMEの利用による幾つかの有機・無機分子のシュレーディンガー解の計算
[利用課題責任者]
量子化学研究協会研究所
中辻 博 研究所長
[利用カテゴリ]
カテゴリB
本課題では、原子・分子系のシュレーディンガー方程式を正確に解く理論: Free Complement - Local Schrödinger Equation (FC-LSE) 法を、有機化学の基礎的分子に適用した。化学の特性に基づく波動関数の効率的記述法: From Atom to Molecule (FATM) 法と、Order-Nを自然に実現し得る電子の反対称化法: Increasing exchange (iExg) 法を初めて導入した。これらの方法は、一般の有機分子の「シュレーディンガー解」の計算を実現するうえで高い一般性と有用性を持っている。TSUBAMEの並列パワーを利用し、実際の分子の精密計算だけでなく、この新しい方法論の検証とプログラム開発も効率的に進められた。適用した分子は大きなものではないが、既存の量子化学理論よりも十分に高い精度の解を得ることができた。また、申請時の予定では、もし可能なら程度に考えていたベンゼン分子のテスト計算まで実行することができた。並列化効率は超パラレルの結果が得られ、高い並列化性能が確認できた一方、単体でのチューニングの必要性が示唆された。
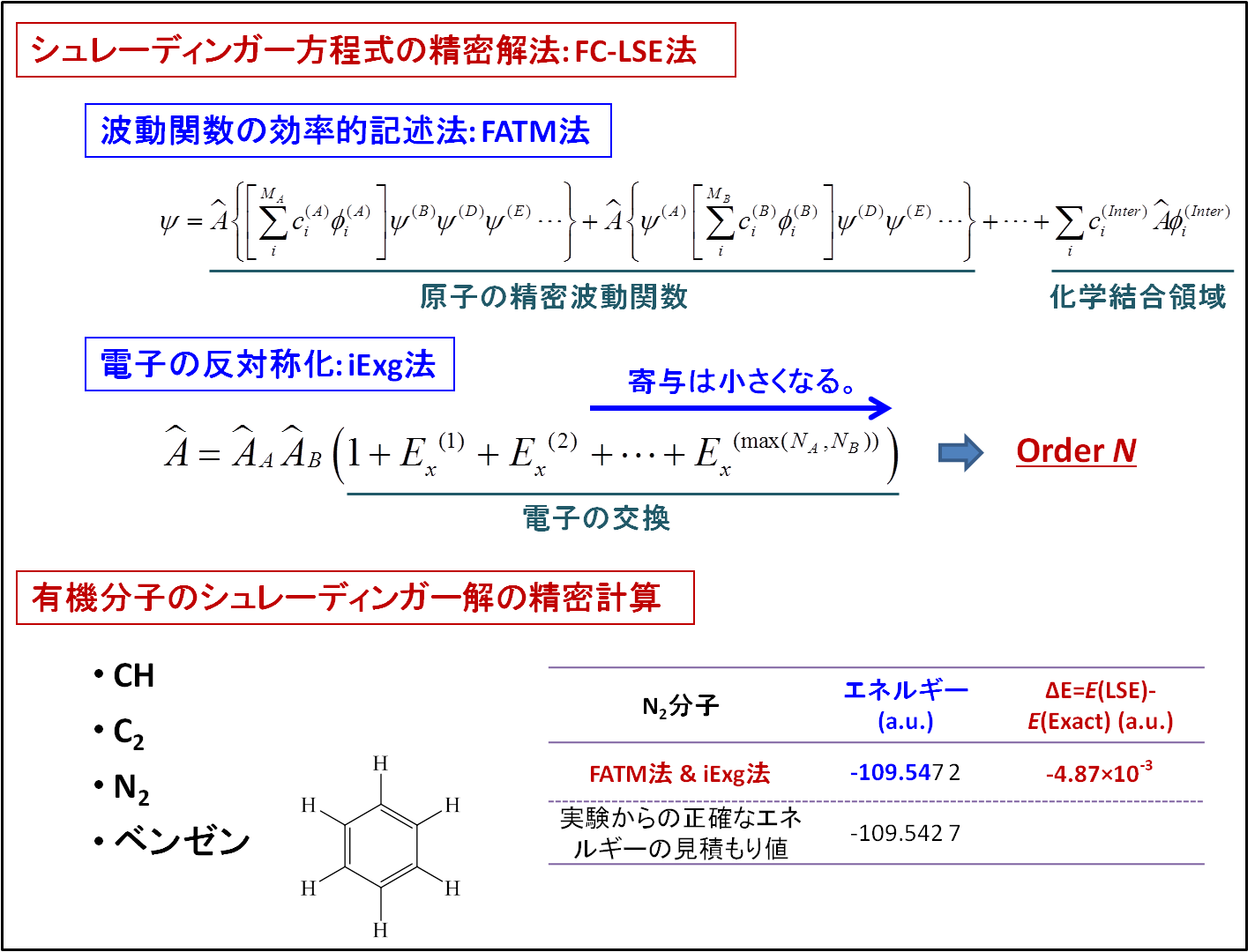
Figure FC-LSE-iExg法による有機分子のシュレーディンガー解の計算
超大規模半正定値計画問題に対する高性能汎用ソルバの開発と評価
[利用課題責任者]
中央大学理工学部
藤澤 克樹 教授
[利用カテゴリ]
カテゴリA (全ノード利用)
半正定値計画問題(SDP)は組合せ最適化, システムと制御, データ科学, 金融工学, 量子化学など非常に幅広い応用を持ち、現在最適化の研究分野で最も注目されている最適化問題の一つとなっている。
SDP に対しては高速かつ安定した反復解法である内点法アルゴリズムが存在しているが、巨大な線形方程式系の計算(行列要素の計算と行列のCholesky分解)が大きなボトルネックとなっている。今回の実行においては申請者らが開発したソフトウェア SDPARA の拡張を行い、多数GPU の活用や計算と通信のオーバーラップ技術を応用することによって、主要なボトルネックの1つである線形方程式系のCholesky 分解の高速化と世界最大規模の SDP(図1) を高速に解くことに成功した(最大で1.018PFlopsの性能を達成 : 図4)。今回の実施では疎性の追求、計算量やデータ移動量などによる計算方法の自動選択などの技術によって、入力データから密と疎な部分が自動的に抽出され、前者は主に GPU、また後者は密データに変換後に CPU アフィニティやメモリインターリーブ技術等(図2と図3)によって CPUコアで高速に大規模並列処理されることを検証し、様々な応用問題に対して SDPARA が高性能な汎用ソルバであることを示した。
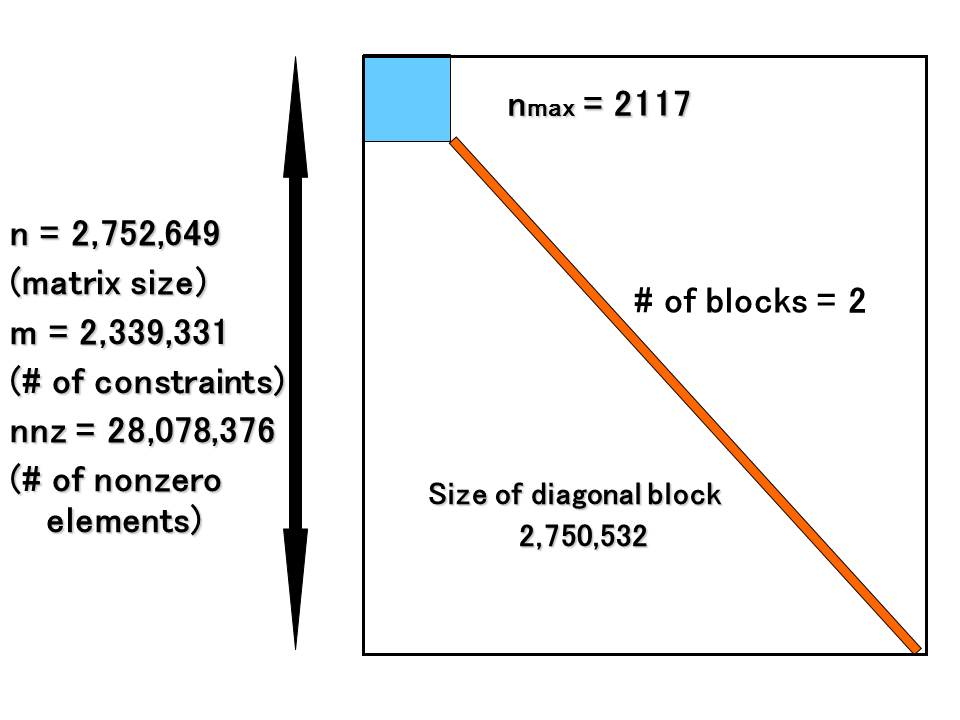
図1 世界最大規模のSDPとそのブロック対角構造
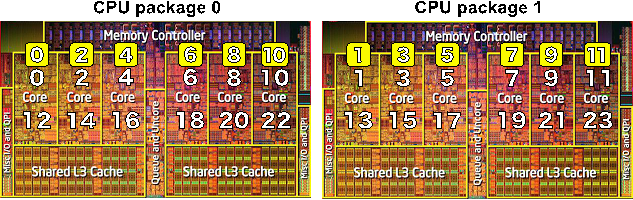
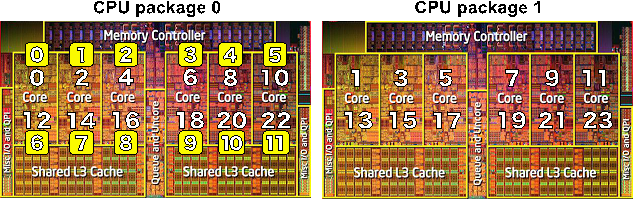
図2 CPU アフィニティの設定方法(scatter タイプと compactタイプ)
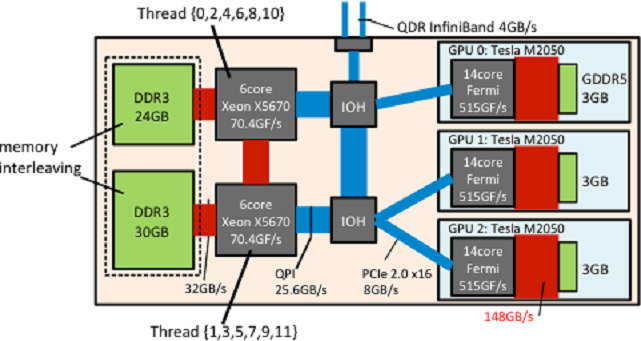
図3 TSUBAME 2.0 の各ノード(HP SL390s) におけるCPU アフィニティの設定とメモリインターリービング
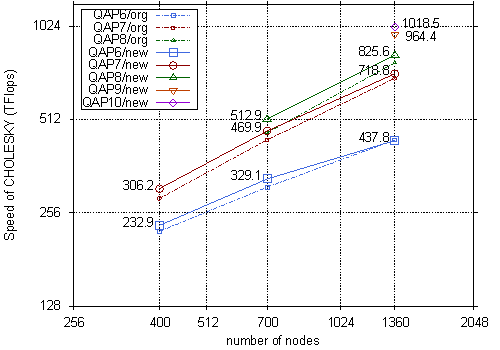
図4 TSUBAME2.0 上でのCholesky分解の性能(1,360ノード, 4,080 GPU)
![[GSIC]東京工業大学学術国際情報センター(学際大規模情報基盤共同利用・共同研究拠点)](../_img/logo.jpg)




