Urgent Info
- There is no Urgent Info now.
GSIC
| Addr. | 2-12-1 O-okayama, Meguroku, Tokyo 152-8550 JAPAN |
| Contact this mail address. |
You are here
Large scale Phase-Field simulation for metal dendritic solidification by multi-GPU computing
Primary Investigator Takayuki Aoki, GSIC, Tokyo Institute of Technology
(taoki[at]gsic.titech.ac.jp)
Collaborator Takashi Shimokawabe, Tokyo Institute of Technology
Collaborator Tomohiro Takaki, Kyoto Institute of Technology
Collaborator Akinori Yamanaka, Tokyo Institute of Technology
Background
The mechanical properties and performance of metal materials depend on the intrinsic microstructures in these materials. In order to develop engineering materials as expected and to enable design with multifunctional materials, it is essential to predict the microstructural patterns, such as dendritic structures, observed in solidified metals. In materials science and related areas, the phase-field method is widely used as one of the powerful computational methods to simulate the formation of complex microstructures during solidification and phase transformation of metals and alloys. The phase-field model consists of a relatively large number of complex nonlinear terms compared with other stencil computation such as advection calculations and diffusion calculations, requiring larger computational power than other stencil applications. Due to this heavy computational load, previous attempts known to us are limited in grid sizes (e.g., 500x500x500 ) and simulated simple shape such as a single dendrite. To evaluate more realistic solidification with phase-field simulations, it is essential to perform large-scale computation reaching 5000x5000x5000 mesh to describe multiple dendrites in the typical scales of microstructural pattern.
Methodology
The phase-field model introduces a continuous order parameter, i.e., a phase-field variable, to describe whether the material is solid or liquid. Solid and liquid are represented as the fixed values of this parameter. Interfaces between solid and liquid are treated as diffuse interfaces, which are given by the localized regions where this parameter changes smoothly between these two fixed values. Thanks to this approach, the phase-field method can describe the locations of the interfaces without introducing the explicit tracking of moving interfaces during microstructure evolution.
The time integration of the phase field variable and the solute concentration are carried out by the second-order finite difference scheme for space with the first-order forward Euler-type finite difference method for time on a three-dimensional regular computational grid. Figure 1 shows that 19 neighbor elements of the phase field variable and seven neighbor elements of the solute concentration are used to compute the government equations on a grid point (i, j, k). We need to read 26 elements from the memory and write back two updated values to the memory for each point of the grid in one time step.
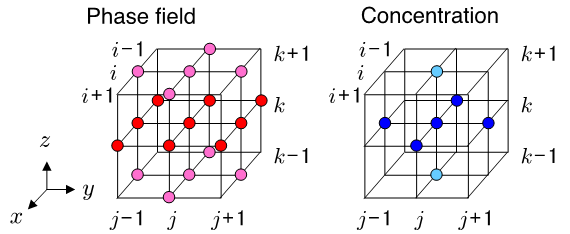
Figure 1 Spatial access patterns of the neighbor points for the phase field variable and the concentration
Description of multi-GPU computing and implementation
We decompose the whole computational domain in both y- and z-directions (2D decomposition) and allocate each subdomain to one GPU. We have chosen this method since 3D decomposition, which looks better to reduce communication amount, tends to degrade GPU performance due to complicated memory access patterns for data exchanges between GPU and CPU. Similar to conventional multi-CPU implementations with MPI, our multi-GPU implementation requires boundary data exchanges between subdomains. Because a GPU cannot directly access to the global memory of other GPUs, host CPUs are used as bridges for data exchange. For inter-node cases, this data exchange is composed of the following three steps: (1) the data transfer from GPU to CPU using CUDA APIs such as cudaMemcpy, (2) the data exchange between nodes with MPI, and (3) the data transfer back from CPU to GPU with CUDA APIs. Based on the above discussion, the first method for multi-GPU, named (a) GPU-only method, is implemented. However, this basic method suffers from costs of three-step data transfer described above. Their impact gets larger when we use more GPUs. In order to improve scalability, hiding such costs by overlapping communication and computation is effective. We present two methods both of which adopt overlapping techniques: (b) Hybrid-YZ method and (c) Hybrid-Y method. Both methods enable overlapping by treating boundary regions separately from an inside region in that both GPUs and CPUs cooperatively participate in computation to improve effects of overlapping.
In our implementation on TSUBAME 2.0, we determined the number of used CPU cores as follows. Since each node has twelve CPU cores (two 6-core Xeon CPUs), we assign four cores to each of three GPUs. Thus each subdomain is cooperatively computed by a single GPU and four CPU cores. CPU code is compiled with Intel C++ Compiler 11.1.072, and multi cores are exploited by using OpenMP.
Results
The weak scaling results of our phase-field simulations running on TSUBAME 2.0 is shown in Fig.2 and It is found the computation linearly scales to 4000 GPU. We choose each GPU handles the domain of 4096x128x128. A snapshot of the dendritic growth is exhibited in Fig.3. The performance evaluation has successfully demonstrated that strong scalability is improved by using our overlapping techniques; with 4,000 GPUs with 16,000 CPU cores, the performance reaches 2.0000045 PFlops for a mesh of 4,096x6,500x10,400, which is the first over peta-scale result as a real stencil application we know to date.
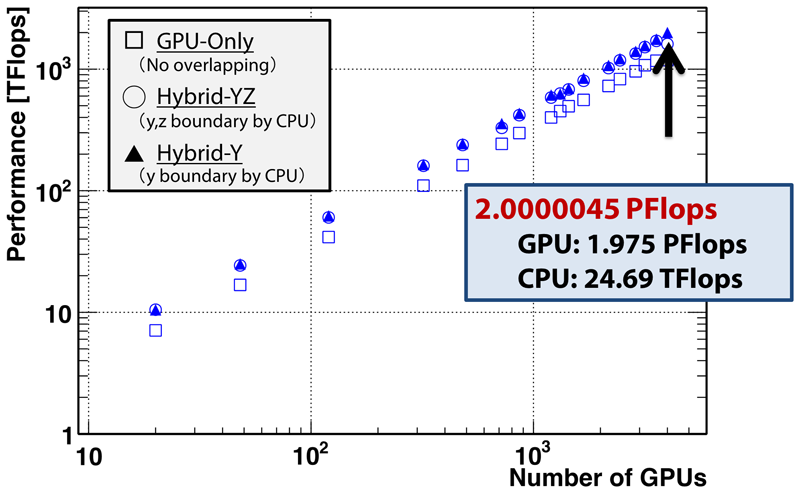
Figure 2 Weak Scaling of multi-GPU computation in both single- and double- precision calculation on TSUBAME 2.0.

Figure 3 Dendritic growth in the binary alloy solidification with 768x1632x3264 mesh using 1156 GPUs of TSUBAME 2.0.
![[GSIC] Tokyo Institute of Technology | Global Scientific Information and Computing Center](../../_img/logo_en.jpg)